
현재 추천 시스템이 적용되고 있고 고도화를 진행하고 있는 시점에서 최근 팀원분들과 추천 스터디를 플립러닝(flipped learning) 방식으로 진행하게 되었습니다. 우선 팀원들과 함께 추천의 내재적인 부분과 기본적인 내용들을 확인하고 놓칠 수 있는 부분들을 점검하고 있습니다.
이번주는 팀원들과 함께 중소형 트래픽 규모를 가진 이커머스 상의 특정 페이지(e.g., 카트 페이지, 상품 상세 페이지)에서 마케팅 캠페인의 요소로 활용될 수 있는 연관분석(Apriori/FP-Growth)에 이어서 CF를 활용한 추천의 두 가지 방식인 User2User와 Item2Item을 큰 틀에서 살펴본 후 실무에서 발생한 여러 이슈들과 앞으로의 실험할 것들에 관하여 토의해보았습니다.
Collaborative Filtering
Check Sparsity
협업 필터링 모델은 ‘비슷한 것을 선호하는 사람들은 이와 유사한 사람들이 선호하는 다른 상품들을 좋아할 수 밖에 없다’는 자명한 명제를 전제합니다. 이것은 필연적으로 User와 Item 사이의 Matrix가 생성되고 생성된 행렬 사이에 비어 있는 부분을 올바르게 채우는 문제[Matrix Completion]로 변환됩니다. 신기한 점은 이 전제를 바라보는 다양한 관점들과 도메인의 개별적인 특성이 더해져서 일반적인 추천 태스크를 풍부하게 만든다는 것입니다. 앞에서 언급한 것처럼 이커머스의 데이터를 활용한 추천 시스템을 고려하였습니다. 어느 사이트 내에서 상호작용한 데이터의 결과가 다음과 같습니다.
1
2
3
4
5
6
view Unique item length : 434
cart Unique item length : 144
Purchase Unique item length : 133
view & cart item length : 144
view & purchase item length : 133
cart & purchase item length : 133
이 경우 해당 사이트의 설계가 아래의 같이 되어 있음을 알 수 있습니다. 다시 말해서 도중에 나갈 수는 있지만 큰 틀은 정해져 있음을 알 수 있습니다.
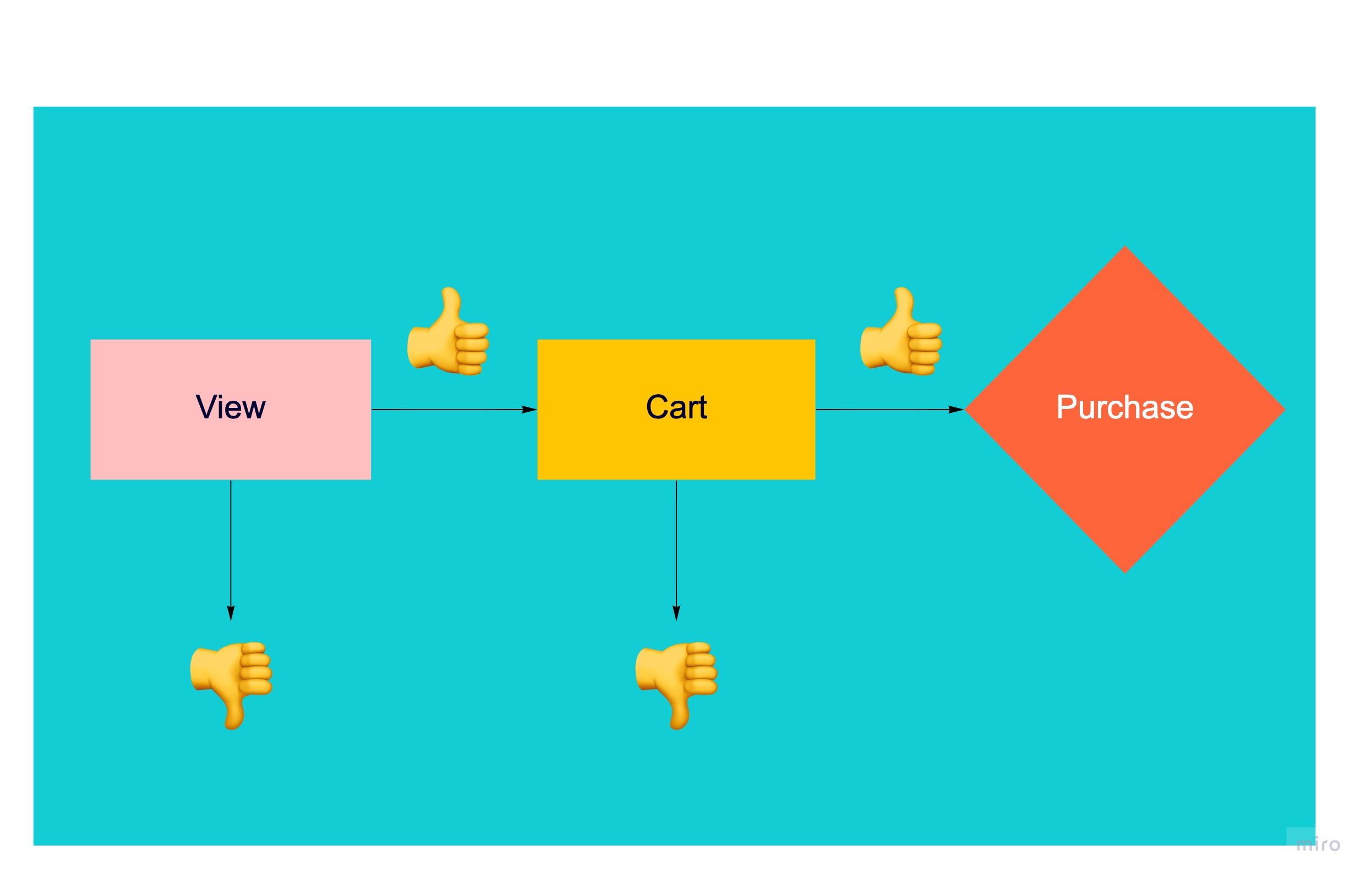
위의 내용과 더불어 직관성을 위해 고객의 상품을 본 로그 데이터만을 활용하겠습니다. 우선 추천에 있어 중요한 이슈인 Sparsity를 살펴보았습니다. 고객이 본 제품 수에 대한 kde plot(Kernel Density plot)을 살펴보니 얼마나 관심받는 제품이 쏠려 있는지 확인할 수 있습니다.
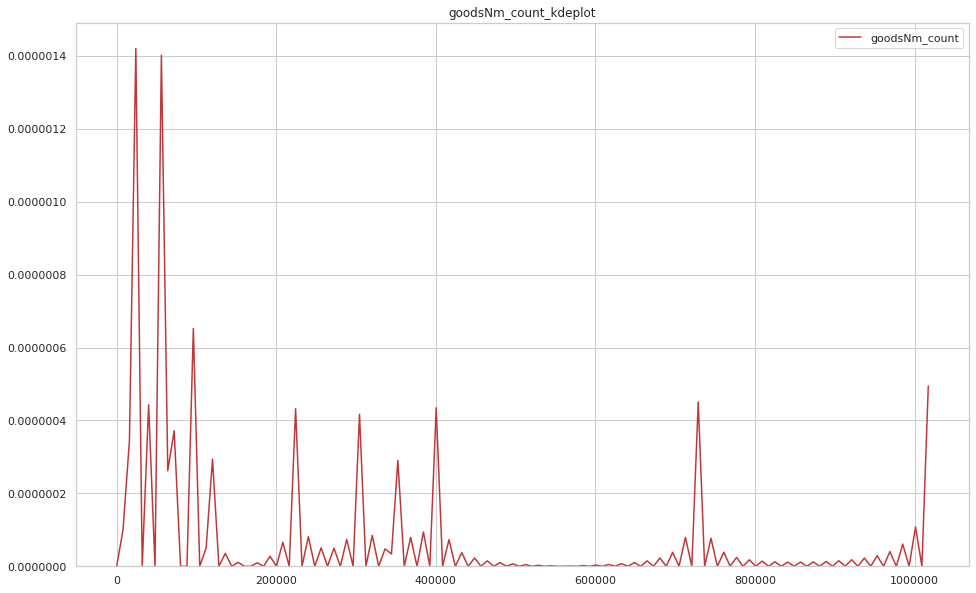
이러한 경향은 구매나 장바구니 데이터에서 더 심할 것입니다. SKU가 풍부한 고객사일 수록 보통 고객들이 상품을 클릭하거나 구매하는 경우는 아주 조금이고 User-Item Matrix는 거의 대부분이 비어있을 것입니다. 부정적[Negative] 관찰이 긍정적[Postive] 관찰보다 훨씬 큰 경우 추천 모델이 과적합될 가능성이 굉장히 높습니다. 무엇보다 위의 그래프에서 알 수 있듯이 Implicit data는 Explicit feedback data에 비해 노이즈가 발생할 가능성이 높아 상품에 대한 긍부정의 판단을 확신할 수가 없습니다.
유사성에 대한 정량화
앞의 협업 필터링에 관한 전제가 너무 추상적이지 않나요? 같은 공간안에서 활동한 데이터[Implicit data]를 활용하여 고객 또는 아이템의 유사성을 어떻게 알 수 있을까요? 어떤 것을 보거나 카트 페이지에 담거나 사는 행위를 방향을 가진 값인 벡터로 전제하면 유사도에 관한 다양한 정량화를 시도할 수 있습니다. 이 때 유사성을 판단하는 데 많은 함수들이 존재합니다. 우선 가장 많이 쓰이는 유클리드 유사도와 코사인 유사도를 간단한 예시를 통해 비교해 보았습니다.
Euclidean Similarity vs Cosine Similarity
우선 평균이 3, 표준편차가 2인 정규분포(->label 0)와 평균이 10, 표준편차가 2인 정규분포(->label 1)를 가정한 후 표본을 10개 뽑아 시각화하면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
length = 10
mu1,sigma1 = 3,2
mu2,sigma2 = 10,2
rand_norm1 = np.random.normal(mu1,sigma1,size=length)
rand_norm2 = np.random.normal(mu2,sigma2,size=length)
rand_norm3 = np.random.normal(mu1,sigma1,size=length)
rand_norm4 = np.random.normal(mu2,sigma2,size=length)
g1 = pd.DataFrame({'x' : rand_norm1,
'y' : rand_norm3,
'label' : [0]*length})
g2 = pd.DataFrame({'x' : rand_norm2,
'y' : rand_norm4,
'label' : [1]*length})
g = pd.concat([g1,g2]).reset_index().drop('index',axis=1)
g2 = pd.DataFrame([g.iloc[9],g.iloc[1],g.iloc[4],g.iloc[11]],
columns = ['x','y','label'])
plt.figure(figsize = [16,10])
sns.set(style = 'whitegrid',palette = 'RdBu')
sns.scatterplot(x = 'x', y ='y',hue='label',data = g)
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
x y label
0 3.900308 -0.153690 0
1 3.216447 2.429164 0
2 2.440244 -0.685625 0
3 3.271666 -0.277008 0
4 5.382853 5.783382 0
5 1.336026 3.859837 0
6 6.001719 3.274914 0
7 2.691871 0.437643 0
8 2.747666 1.021616 0
9 2.341537 1.949354 0
10 8.436320 10.688145 1
11 8.966173 12.389481 1
12 5.268006 11.766504 1
13 8.044761 8.574096 1
14 10.734666 11.776260 1
15 7.045491 11.774815 1
16 10.799736 9.969498 1
17 9.924590 11.245653 1
18 8.045663 10.805871 1
19 8.908425 7.761628 1
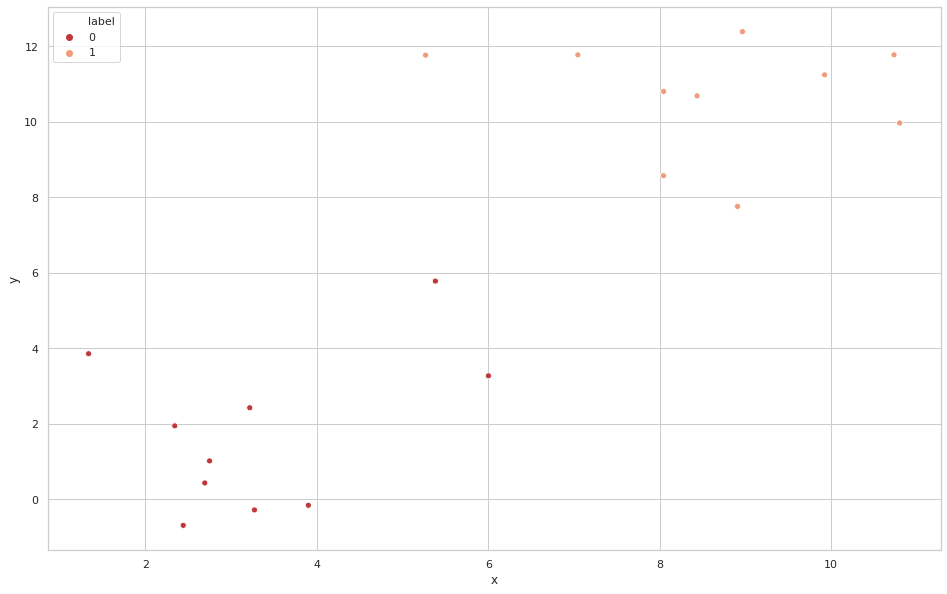
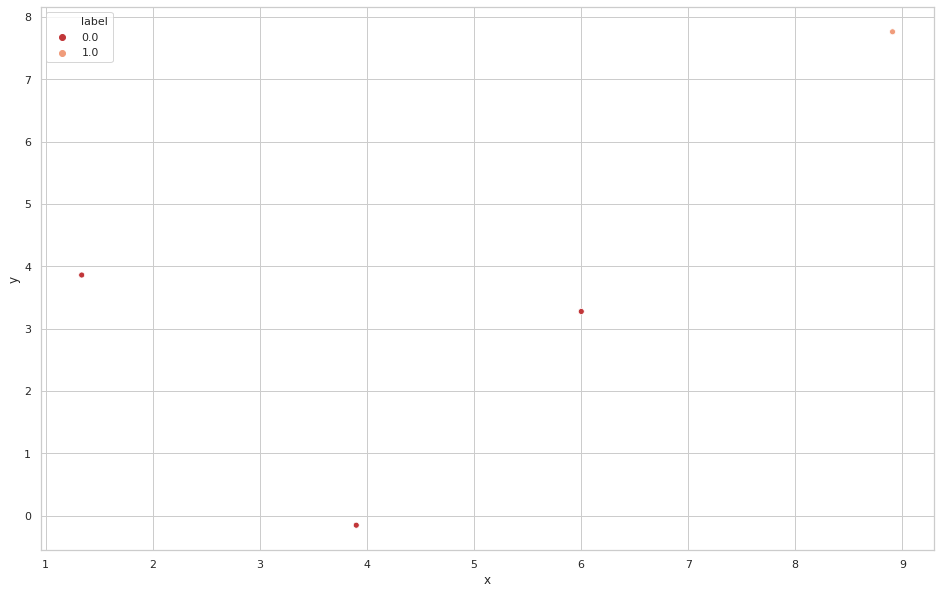
비교를 명확히 하기 위해 인덱스가 0,5,6,19을 따로 뽑아 시각화하면 다음과 같습니다.
1
2
3
4
g2 = pd.DataFrame([g.iloc[0],g.iloc[5],g.iloc[6],g.iloc[19]],columns = ['x','y','label'])
plt.figure(figsize = [16,10])
sns.set(style = 'whitegrid',palette = 'RdBu')
sns.scatterplot(x = 'x', y ='y',hue='label',data = g2)
1
2
3
4
5
6
7
8
9
10
g2 = pd.DataFrame([g.iloc[9],g.iloc[4],g.iloc[11]],
columns = ['x','y','label'])
g3 = pd.DataFrame([g.iloc[1]],columns = ['x','y','label'])
plt.figure(figsize = [16,10])
ax = g2[g2['label'] == 0].plot.scatter(x='x',y='y',label='1')
ax = g2[g2['label'] == 1].plot.scatter(x='x',y='y',label='2',ax=ax)
ax = g2[g2['label'] == 2].plot.scatter(x='x',y='y',label='3',ax=ax)
ax = g3.plot.scatter(x='x',y='y',label='not defined',c = 'gray',ax=ax)
ax
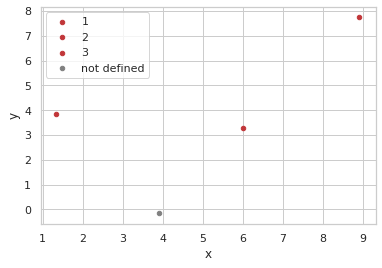
유클리드와 코사인 유사도의 정의는 다음과 같습니다.
이것을 기반으로 구체적인 거리를 구하면 다음과 같습니다.
1
2
3
4
5
6
def euclidean_distance(x, y):
return np.sqrt(np.sum((x - y) ** 2))
print('g[5] & g[0] : ',euclidean_distance(np.array(g2.iloc[0])[:-1],np.array(g3.iloc[0])[:-1]))
print('g[6] & g[0] : ',euclidean_distance(np.array(g2.iloc[1])[:-1],np.array(g3.iloc[0])[:-1]))
print('g[19] & g[0] : ',euclidean_distance(np.array(g2.iloc[2])[:-1],np.array(g3.iloc[0])[:-1]))
1
2
3
g[5] & g[0] : 4.7627656335300985
g[6] & g[0] : 4.021350544947775
g[19] & g[0] : 9.366616569117832
1
2
3
4
5
6
def cosine_similarity(x, y):
return np.dot(x, y) / (np.sqrt(np.dot(x, x)) * np.sqrt(np.dot(y, y)))
print('g[9] & g[1] : ',cosine_similarity(np.array(g2.iloc[0])[:-1],np.array(g3.iloc[0])[:-1]))
print('g[4] & g[1] : ',cosine_similarity(np.array(g2.iloc[1])[:-1],np.array(g3.iloc[0])[:-1]))
print('g[11] & g[1] : ',cosine_similarity(np.array(g2.iloc[2])[:-1],np.array(g3.iloc[0])[:-1]))
1
2
3
g[5] & g[0] : 0.2896332523594205
g[6] & g[0] : 0.8582781242557574
g[19] & g[0] : 0.7275194576696773
위의 예시에서 알 수 있듯이 어떤 유사도 측도를 사용하는가에 따라서 최종적으로 추천되는 상품이 다를 수 있음을 알 수 있습니다. 식의 정의와 함께 생각해 보았을 때 유클리드 거리 측도는 두 상품간의 각도는 고려하지 않고 두 상품 벡터가 위치한 좌표상의 거리만을 고려합니다. 그러므로 최소 거리인 0부터 무한대까지의 범위를 가집니다.
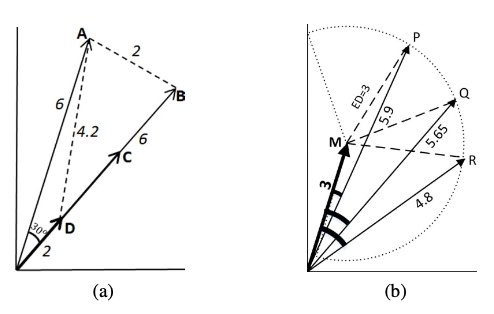
위의 예시와 그림을 통해 알 수 있듯이 코사인 유사도를 측도로 사용할 경우 최솟값은 -1이고 최대값은 1입니다. 이 경우 벡터의 크기를 고려하지 않고 상품의 비율을 고려하여 측정합니다.
벡터의 크기와 비율을 고려한 측도인 TS-SS와 여러 유사도 과련 측도들이 연구되고 있습니다. 관습적으로 많이 사용하는 현재의 상품 유사도 측도와 더불어 다양한 상품 유사도 실험을 상품 벡터를 만드는 다양한 데이터 전처리 방법 및 이커머스 도메인의 특성을 결합하여 진행하면 재밌고 의미있는 결과를 알 수 있을 것 같습니다.
협업 필터링에 관한 네가지 접근 방법
크게 협업 필터링은 Memory-Based CF(Collaborative Filtering 이하 CF)와 Model-based CF로 나눌 수 있습니다. 그리고 Memory-Based CF와 Model-based CF를 적절히 섞은 Hybrid CF 방법도 존재합니다. 최근에는 비선형적인 심층 신경망 모델을 활용하여 Matrix Factorization을 일반화하거나 순서를 반영하는(Sequence-aware) 추천 시스템 연구 결과들이 많이 나오고 있는 동시에 전통적인 협업 필터링과 비교했을 때 위의 기법들의 실효성에 의문을 가지는 연구 결과도 있습니다. 이 모든 내용을 한 포스트에 담는 것은 실용적이지 못합니다.
우선 Memory-Based CF와 Model-based CF를 살펴보겠습니다. 경사하강법과 같은 모수에 대한 최적화를 활용하는 Model-based CF와는 다르게 Memory-Based CF는 단순히 산술 연산만을 사용합니다.
Memory-Based CF는 User-item filtering과 item-item filtering으로 다시 나눌 수 있습니다. user-item 필터링은 특정한 유저를 취한 후 상품의 기호가 유사한 고객들을 찾은 뒤 유사한 고객들이 좋아한 다른 상품들을 추천합니다. 이와 반대로 item-item filtering은 특정한 아이템을 선택한 후 이 아이템을 좋아하는 다른 고객들이 선호하는 상품들을 최종적으로 추천합니다.
일차적으로 메모리 기반의 협업 필터링과 모델 기반의 협업 필터링을 섞은 모델과 개별적인 각각의 모델(메모리 기반 모델 / 모델 기반 협업 필터링)을 고안하고 객관적인 지표를 선정하여 특정 도메인의 이커머스 사이트에서 가장 효과적인 모델을 비교하는 실험을 진행하면 흥미로울 것 같습니다.
Reference
- Apriori and FP-Growth Description
- Recommendation System for E-commerce using Collaborative Filtering
- Flipped Learning
- Collaborative Filtering in Wikipedia
- Matrix Completion in Wikipedia
- TF-IDF description
- Various Implementations of collaborative Filtering
- Intro to Recommender systems:Collaborastive Filtering
- T-Academy for recommendation system
- Content Based Filterintg & Collaborative Filtering
- Collaborative Filtering for Implicit Feedback Datasets
- A Hybrid Geometric Approach for Measuring Similarity Level Among Documents and Document Clustering
- Logistic Matrix Factorization for Implicit Feedback Data
- 9 Distance Measures in Data Science
- Euclidean & Cosine Distance
- TS-SS description
- Vector Similarity
- Kernel-Mapping Recommender system algorithms
- Are we really making much progress? A worrying analysis of recent neural recommendation approaches
- Performance comparison of neural and non-neural approaches to session-based recommendation
