Kernel Density Estimation

sphere_space

현실에서 마주한 문제

현재 제가 속한 팀은 개별 고객의 구매 확률을 예측하여 고객을 자동으로 세분화(Auto Customer Segmentation)하는 태스크를 진행하고 있습니다. 머신러닝 모델을 활용하여 각 고객이 해당 사이트를 방문한 후 구매를 할 확률값을 알 수 있습니다. 이 확률값들의 분포를 Histogram을 활용하여 고객이 쉽게 파악할 수 있도록 기획하였습니다.
하지만 Histogram을 사용할 경우 ‘bin의 갯수와 크기를 어떻게 주는가’에 따라 모양이 다르게 보이는 문제가 있었습니다. 그리고 무엇보다 bin의 경계에서 필연적으로 연속적이지 않은 점을 발견하였습니다. 이 점은 그래프를 보는 분들로 하여금 직관적이지 않으면서 잘못된 판단을 내릴 수 있습니다.
이러한 Histogram의 문제를 Smoothing 효과로 완화시킬 수 있는 KDE(Kernel Density Estimation) plot으로 해결할 수 있었습니다. 실무에 적용하였던 KDE에 대한 내용물을 공유하고자 합니다.

무엇을 알고 있나?

기본적으로 저는 다음을 알 수 있었습니다.

특정한 실험 환경을 제외하고 R.V(Random Variable)이 발생할 수 있는 모든 경우에 접근할 수 없습니다. 다시 말해서 정확한 확률 변수의 분포를 알 수 없습니다. 우리는 다만 ‘확률 변수’가 현실에서 보여주었던 활동에 대한 기록(Data)은 가지고 있습니다. 현재 설정된 확률변수는 구매 확률(“Purchase Probability”)입니다.

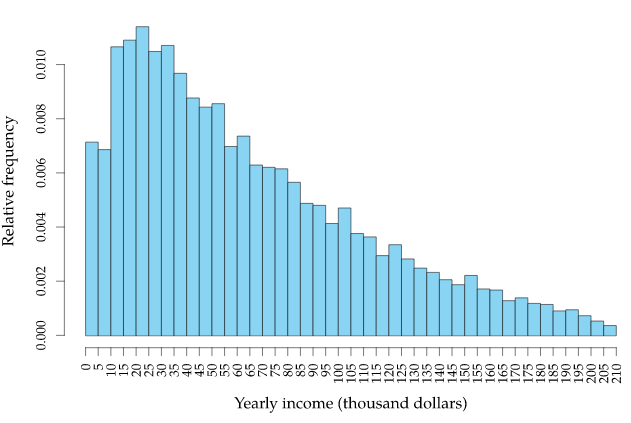
우선 Histogram이 어떤 특성을 가지고 있는지 확인해 보았습니다. 먼저 bin이 많아짐에 따라 Histogram의 변화 양상을 간단한 실험을 통해 파악해보았습니다.

구체적인 실험의 세팅은 다음과 같습니다.

평균이 0이고 표준편차가 1를 따르는 표준정규분포에서 크기가 10000인 표본을 생성합니다.
이때 재현성(Reproductivity)을 위해서 seed값은 고정합니다.
bin의 갯수를 5에서 30까지 5의 단위로 나눈 후 앞에서 생성한 표본에 대한 히스토그램을 생성합니다.

mu,sigma,size = 0,1,10000
np.random.seed(seed = 37)
normal_obj = np.random.normal(mu,sigma,size)
print('size = {}, mean = {}, std = {}'.format(len(normal_obj),np.mean(normal_obj),np.std(normal_obj)))

size = 10000, mean = 0.0017234068142374496, std = 0.9952894925656007

bins_candidate = [i for i in range(5,35,5)]
plt.rcParams['figure.figsize']=(16,10)
len_candidate = len(bins_candidate)

for i in range(1,len_candidate+1,1):
    plt.subplot(2,int(len_candidate/2),i)    
    plt.title('bins(' + str(bins_candidate[i-1]) + ') affect in histogram')
    sns.distplot(normal_obj,
                 kde = False,
                 bins = bins_candidate[i-1],
                 color = 'blue')
plt.savefig('histogram.png')

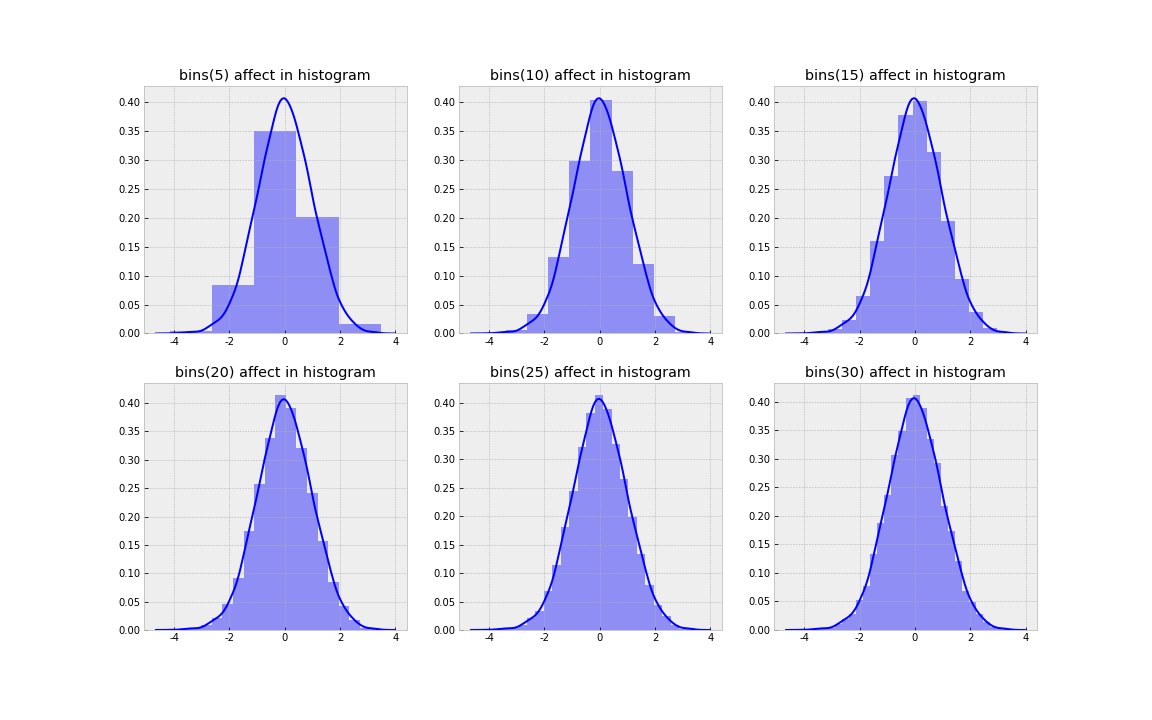
histogram

위의 실험의 결과를 통해 다음과 같은 상황을 알 수 있습니다.

(1) 히스토그램은 관측치를 묶을 bin을 설정한 후 각 bin에 해당하는 사건들의 수를 카운팅한 결과입니다.
(2) bin의 갯수의 조절이 굉장히 중요합니다. 왜냐하면 bin의 갯수에 따라 같은 사건도 히스토그램에서는 다양하게 보여지기 때문입니다.
(3) 이산적인 값들로 bin을 설정하기 때문에 범위 경계값이 같은 값이 아닌 한 서로 단절된 값을 가지게 됩니다.
(4) 히스토그램은 단순히 설정된 bin 범위에 사건들이 모여서 시각화된 것입니다. 다시 말해서 특정한 분포를 가정하지 않았습니다.

밀도 추정(Density Estimation)에 관하여

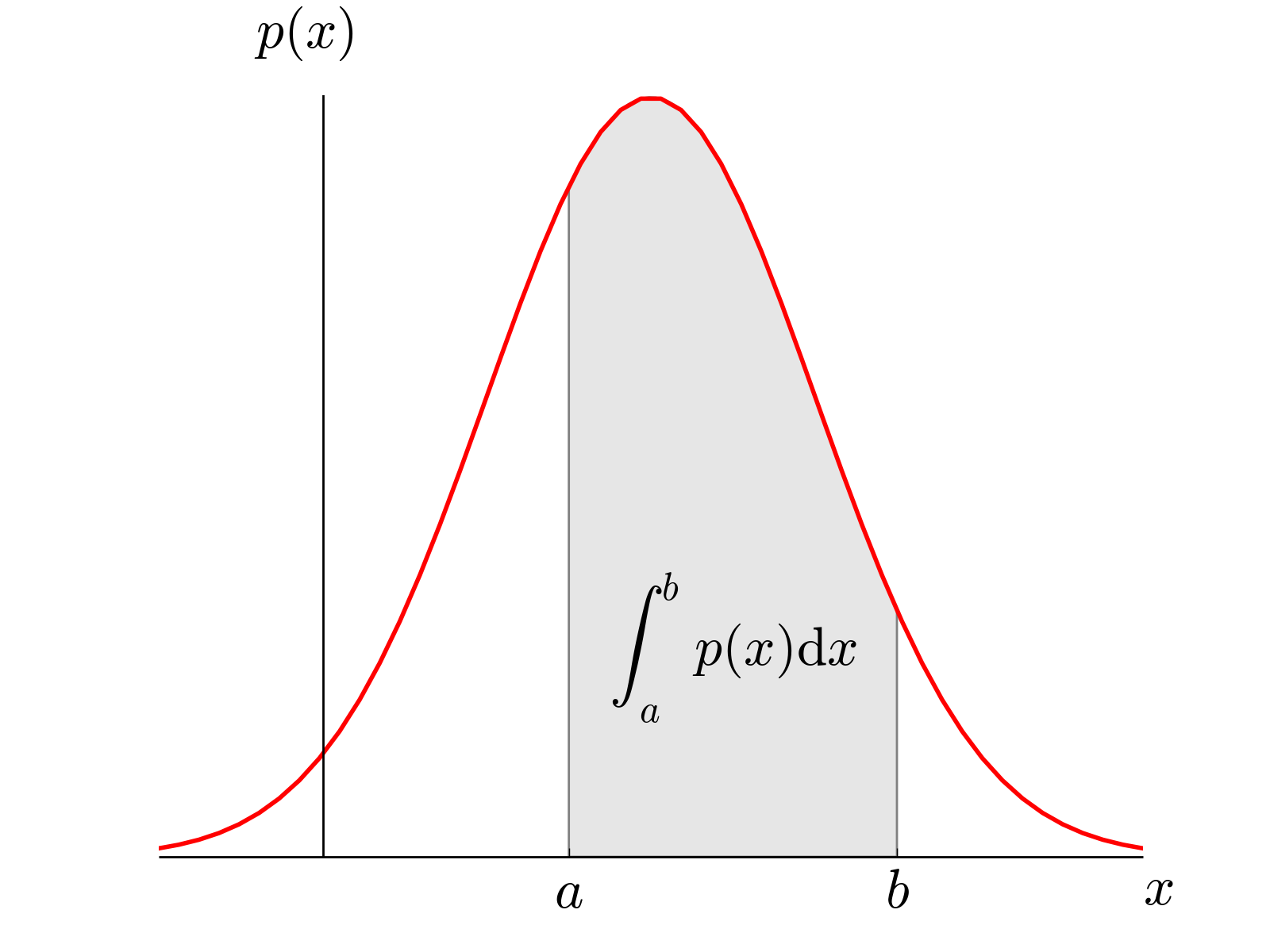
사실 이커머스 분야에서 많은 확률 변수들이 구체적인 값을 가지는 범위는( \(0 \leq X < \infty )\) 입니다. 일정 시간 동안 의미 있는 양의 데이터가 쌓였을 때 관측된 데이터로 원래 확률 변수의 분포를 추정하는 것을 밀도 추정(Density Estimation)이라 합니다. 통계적으로 표현할 때 특정 변수의 밀도를 추정하는 것은 그 변수의 확률 밀도 함수(Pdf, Probability density function)을 추정하는 것과 동치입니다. 하지만 확률(Probability)과 밀도가 같은 개념은 아닙니다. 평균이 양수인 아래의 정규분포를 통해 확률과 밀도의 차이를 살펴볼 수 있습니다.

density_prob http://farside.ph.utexas.edu/teaching/301/lectures/node102.html¹

위의 그래프에서 a부터 b까지의 확률은 다음과 같이 적분값으로 표현할 수 있습니다.

\[\begin{aligned} P(a \leq X \leq b) &= P(a \leq X < b) \\ &= P(a < X \leq b) \\ &= P(a < X < b) \\ &= \int_{a}^b P(x)\,dx \end{aligned}\]

여기서 재밌는 사실을 발견할 수 있습니다. 즉 연속적인 변수의 분포상에서 p(a)와 p(b)는 확률값은 0이지만 밀도값은 상대적인 값[p(a),p(b)]을 가집니다. 다시 말해서 확률밀도함수의 값을 밀도로 말할 수 있고 데이터 분석가가 특정 점의 확률값은 알 수 없지만 특정 범위 내에서 값을 확률밀도함수의 적분값으로 표현할 수 있습니다.

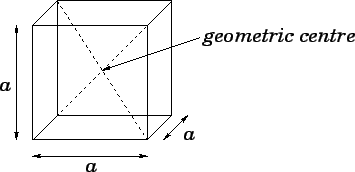qube http://work.thaslwanter.at/Stats/html/_images/PDF.png²

위의 이미지와 같이 실수공간에 속하는 O차원의 W가 있습니다. W에서 어떤 확률밀도함수가 있고 N개의 확률 변수 벡터값이 존재한다고 가정하겠습니다. 이럴 경우 개별적인 벡터가 실수 공간 W에 포함될 확률은 베르누이 분포를 따릅니다. 다시 N개의 벡터중 k개가 실수 공간 R에 포함될 확률은 베르누이 분포의 확장인 이항 분포를 따르므로 다음과 같이 표현할 수 있을 것입니다.

\[P(k)=\left( \begin{matrix} N \\ k \end{matrix} \right) { P }^{ k }(1-P)^{ N-k }\]

이미 우리는 굉장히 익숙한 이항분포의 평균과 분산을 알고 있습니다. 구체적인 평균과 분산을 기술하면 다음과 같습니다.

\[E(k)=NP\] \[Var(k) = NP(1-P)\]

물론 표본평균의 평균과 분산은 다음과 같을 것입니다.

\[E(k)=NP\rightarrow E\left[ \frac { k }{ N } \right] =P\] \[Var(k)=NP(1-P)\rightarrow Var\left[ \frac { k }{ N } \right] =\frac { P(1-P) }{ N }\]

만약 N이 무한대만큼 커진다면 분산이 0으로 수렴함에 따라 첨도가 급속도록 커지는 분포를 쉽게 상상할 수 있습니다.

\[P \cong \frac { k }{ N }\] \[Var\left[ \frac { k }{ N } \right] =\frac { P(1-P) }{ N } \cong 0\] \[P=\int _{ W }^{ }{ P({ x }^{ \prime })d{ x }^{ \prime } } \cong p(x)V=\frac { k }{ N } ,\quad p(x)=\frac { k }{ NV }, V = Volume\]

Parzen window

위에서 명시한 공간 W의 크기가 굉장히 작게 고정시킨 후 확률 밀도 함수를 유도하려 할 때, 샘플링된 데이터가 존재할 경우와 존재하지 않을 경우를 통합하는 수학식은 아래와 같습니다.

\[k=\sum _{ i=1 }^{ N }{ K(\frac { { x }^{ i }-x }{ a } ) }\] \[K(u) = \begin{cases} 1 & |b_{ i }| \le \frac { 1 }{ 2 } \\ 0 & \text{otherwhise} \end{cases}\]

O차원의 cube안에 기준 벡터를 기준으로 \(\frac { a}{ 2 }\) 안에 들어온 모든 샘플수를 세면 됩니다. 앞의 수식과 결합하여 다음과 같은 Parzen window density estimation을 통한 확률 밀도 함수를 도출합니다.

\[p(x)=\frac { 1 }{ N{ h }^{ O} } \sum _{ i=1 }^{ N }{ K(\frac { { x }^{ i }-x }{ a } ) }\]

하지만 아래 그림에서 알 수 있듯이 단순한 Parzen window를 통한 확률 밀도를 추정할 경우 데이터가 이산적인 경우는 큰 상관이 없지만 확률변수가 연속형일 경우 조금 더 유연한 커널 함수가 필요합니다.

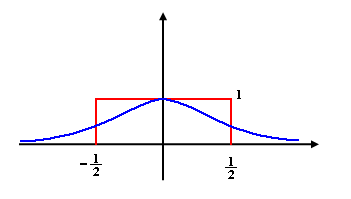parzen_vs_smoothing https://www.projectrhea.org/rhea/index.php/Lecture_16 ³_

다시 말해서 다양한 커널 함수를 문제 상황의 문맥에 맞게 설정하는 것이 중요합니다. 아래 그림은 다양한 커널 함수의 예시를 보여줍니다.

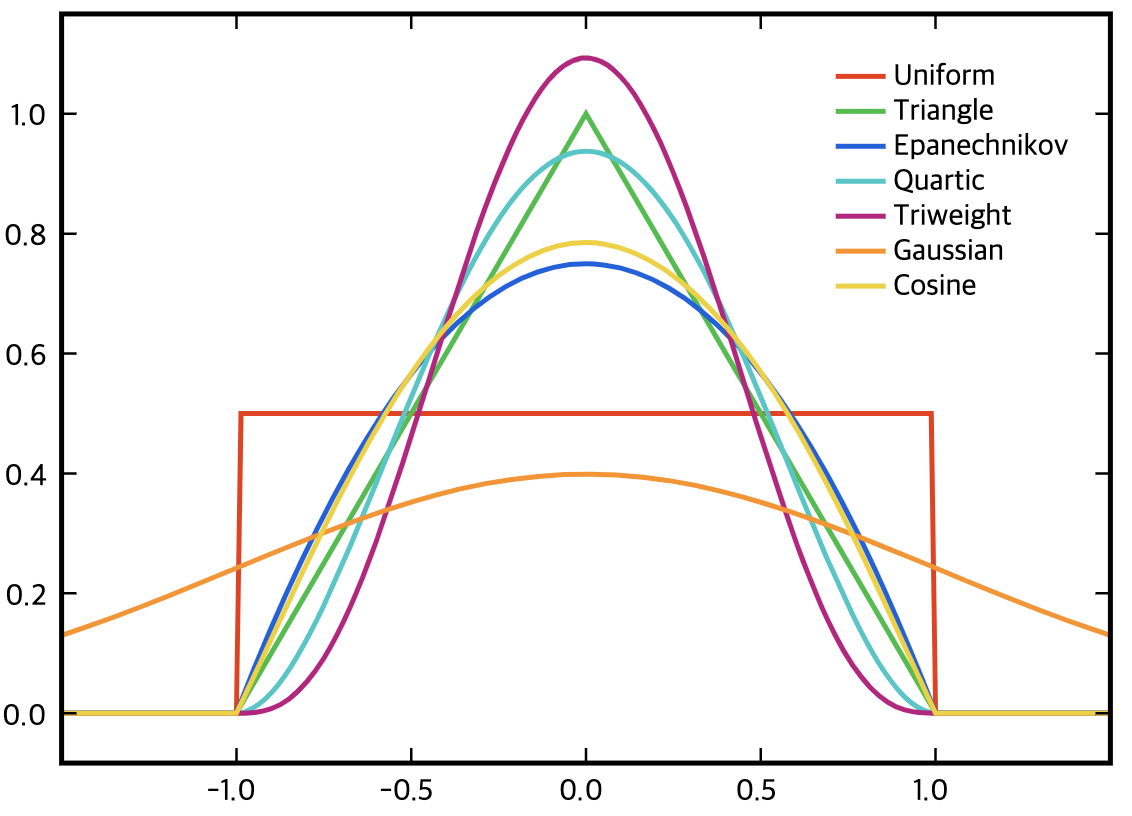
kernel

위의 다양한 커널 함수에서 커널 함수의 몇 가지 특징을 추론할 수 있습니다(사실 앞의 수식들에서 전개되었습니다)

커널 함수는 당연히 전체 구간의 확률 밀도 함수에 대한 적분값이 1입니다.
모든 커널 함수값은 0보다 큽니다.
모든 커널 함수값은 0을 기준으로 대칭입니다.

여기서 공간을 결정하는 a가 하이퍼 파라미터임을 알 수 있습니다. a는 어떤 특징이 있을까요? 실험을 계속 진행해보겠습니다.

Non-parametric Density Estimation

특정한 분포를 가정한 후 해당 데이터의 분포를 찾아가는 방법을 Parametric Density Estimation이라 합니다. 앞에서 실험한 데이터는 모집단이 정규분포를 따르므로 모분포를 정규분포로 가정한 후 데이터의 분포를 추정해도 상관이 없습니다. 물론 아래와 같은 분포(Skewed Distribution)도 존재합니다.

skewd_data_example https://towardsdatascience.com/skewed-data-a-problem-to-your-statistical-model-9a6b5bb74e37⁴

이 경우에는 데이터를 변환(Ex : \(log(x)\), \(\sqrt{x}\))하거나 Box-Cox transform같은 Power Transformation⁵을 적용하여 모수 밀도 추정을 진행할 수 있습니다. 하지만 다음과 같은 경우는 어떻게 될까요? 새로운 실험을 진행해보겠습니다.

먼저 평균이 0이고 표준편차가 1인 표준정규분포와 평균이 4이고 표준편차가 1인 정규분포를 가정합니다.
위의 두 모집단에서 표본 10000개를 추출합니다.

np.random.seed(seed = 37)
def get_normal_data(mu,sigma,size):
    return np.random.normal(mu,sigma,size)

normal_data_mu0 = get_normal_data(0,1,10000)
normal_data_mu4 = get_normal_data(4,1,10000)

print('size = {}, mean = {}, std = {}'.format(len(normal_data_mu0),np.mean(normal_data_mu0),np.std(normal_data_mu0)))
print('size = {}, mean = {}, std = {}'.format(len(normal_data_mu4),np.mean(normal_data_mu4),np.std(normal_data_mu4)))

size = 10000, mean = 0.0017234068142374496, std = 0.9952894925656007
size = 10000, mean = 3.9908289937790324, std = 1.0049462867427261

bins_candidate = [i for i in range(5,35,5)]
plt.rcParams['figure.figsize']=(16,10)
len_candidate = len(bins_candidate)

for i in range(1,len_candidate+1,1):
    plt.subplot(2,int(len_candidate/2),i)    
    plt.title('bins(' + str(bins_candidate[i-1]) + ') affect in histogram')
    sns.distplot(normal_data_mu0,
                 kde = True,
                 bins = bins_candidate[i-1],
                 color = 'blue')
    sns.distplot(normal_data_mu4,
                 kde = True,
                 bins = bins_candidate[i-1],
                 color = 'blue')

우선 히스토그램와 이 글의 핵심 주제인 KDE(Kernel Density Estimation) plot을 시각화하면 다음과 같습니다.

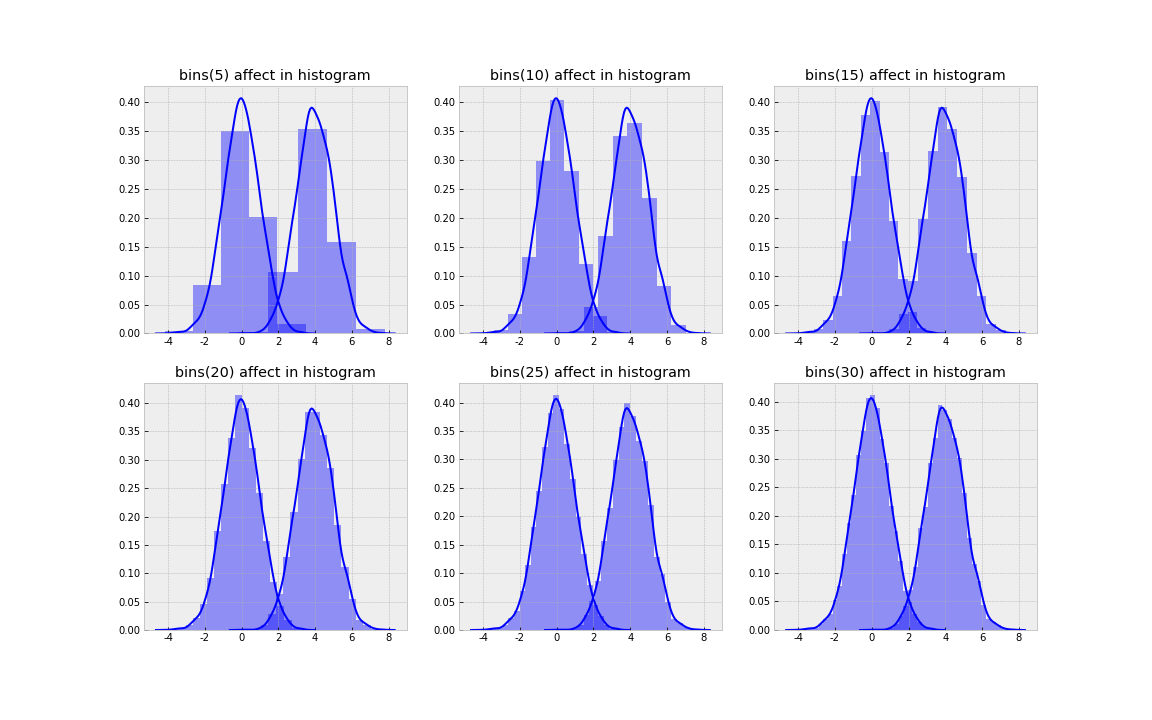
histogram_bimodal_distribution

저는 위의 그래프에서 다음을 발견할 수 있었습니다.

쌍봉분포(Bimodal distribution) 형태를 데이터는 당연히 가집니다.
비모수 밀도 추정을 기반으로 표현되는 경우 모수의 분포를 포착할 수 있지만 단일한 정규 분포를 가정할 경우 모수의 분포와 큰 차이를 가지게 됩니다.

bandwidth의 놀라운 효과

Alt Text

위의 그래프들의 이동으로 살펴볼 때 bandwidth가 높을 수록 커널값이 수평으로 누그러지는 효과를 확인할 수 있습니다.

bandwidth의 효과를 위의 쌍봉분포에 적용해 보겠습니다.

total_data = np.concatenate((normal_data_mu0,normal_data_mu4),axis=0)
x_grid = np.linspace(-4,8,1200)

def kde_value(x, x_grid, bandwidth=0.2, **kwargs):
    """Kernel Density Estimation
    parameters
    __________
    x = sample data
    x_grid = range of x axis
    
    Returns
    __________
    exponential(log_pdf) = exponential(log-likelihood of sample data)
    """
    kde_skl = KernelDensity(bandwidth=bandwidth, **kwargs)
    kde_skl.fit(x[:, np.newaxis])
    log_pdf = kde_skl.score_samples(x_grid[:, np.newaxis])
    return np.exp(log_pdf)
 
plt.rcParams['figure.figsize']=(16,10)
figure,axe = plt.subplots()
for bw in [0.1,0.4,0.7,1]:
    axe.plot(x_grid,kde_value(total_data,
                              x_grid,
                              bandwidth = bw),
             label = 'bandwidth = {}'.format(bw))
    axe.set_xlim(-4,8)
    axe.legend(loc = 'upper right')
axe.hist(total_data,fc = 'blue',alpha = 0.1,normed=True) 

흥미롭게도 결과는 다음과 같습니다.

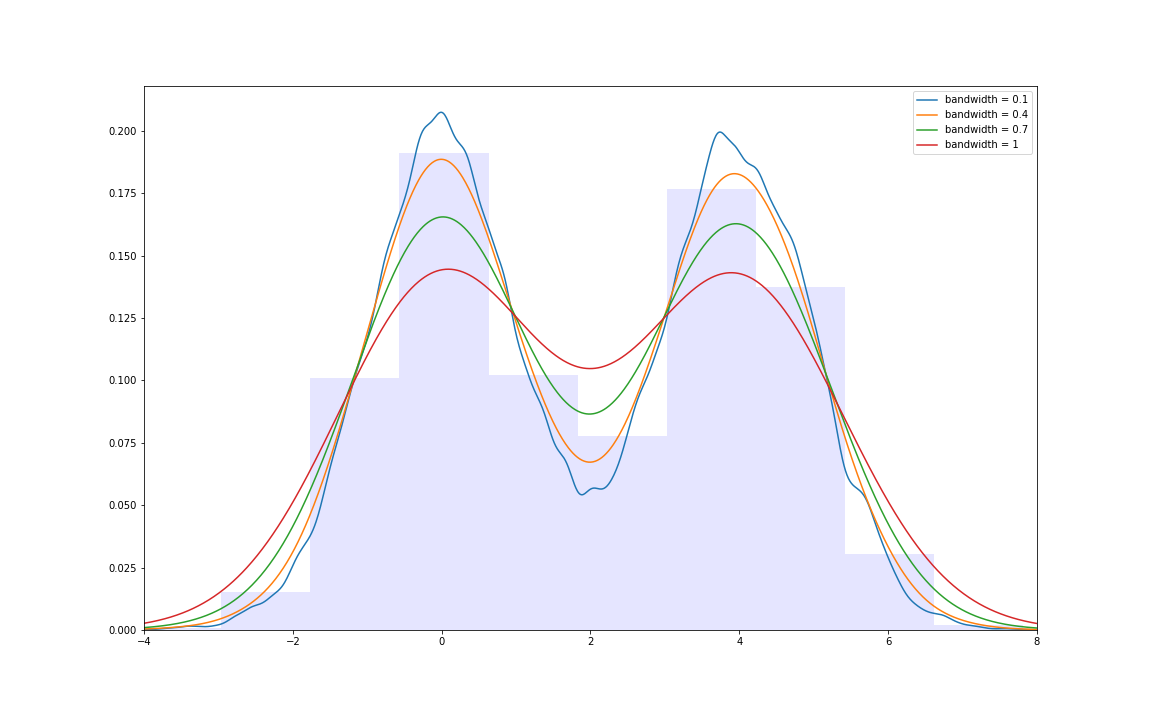
bandwidth_effect

다시 문제로 돌아왔습니다. 히스토그램에서 ‘bin의 경계에서 필연적으로 연속적이지 않는다’라는 문제점은 커널 함수의 도입으로 해결할 수 있습니다. 또한 히스토그램의 Smoothing효과는 적절한 a값을 줌으로써 극대화할 수 있습니다.

물론 공간 W를 단순히 Parzen window로 처리하지는 않을 것입니다. 왜냐하면 지금 표현하고자 하는 확률 변수는 구매확률이고 구매확률은 0에서 100까지 연속적인 값들로 표현할 수 있기 때문입니다. 그래서 저는 가장자리를 장악할 수 있는 다양한 커널들 중 Epanechnikov 커널을 선택하였습니다. Epanechnikov 커널⁶은 다음과 같습니다.

\[EpanK^*(x) = \frac{3}{4}(1-u^2)_+\]

최종적인 코드는 구매 확률을 예측하는 머신러닝 모델의 결과값이 먼저 존재하였으므로 그 결과값에 해당하는 커널 밀도 함수값을 몽고 DB에 넣기 위해서 스파크 코드로 후처리한 후 일차적인 마무리를 지었습니다.

Reference

http://farside.ph.utexas.edu/teaching/301/lectures/node102.html ↩
http://work.thaslwanter.at/Stats/html/_images/PDF.png ↩
https://www.projectrhea.org/rhea/index.php/Lecture_16_-_Parzen_Window_Method_and_K-nearest_Neighbor_Density_Estimate_OldKiwi ↩
https://towardsdatascience.com/skewed-data-a-problem-to-your-statistical-model-9a6b5bb74e37 ↩
https://www.statisticshowto.com/box-cox-transformation/ ↩
https://stats.stackexchange.com/questions/215835/if-the-epanechnikov-kernel-is-theoretically-optimal-when-doing-kernel-density-es ↩

Kernel Density Estimation

현실에서 마주한 문제

무엇을 알고 있나?

밀도 추정(Density Estimation)에 관하여

Parzen window

Non-parametric Density Estimation

bandwidth의 놀라운 효과

Reference

Contents

Trending Tags

Kernel Density Estimation

현실에서 마주한 문제

무엇을 알고 있나?

밀도 추정(Density Estimation)에 관하여

Parzen window

Non-parametric Density Estimation

bandwidth의 놀라운 효과

Reference

Contents

Further Reading

이산형 확률 분포

Fundamentals of DE - 데이터 엔지니어링이란 무엇인가?

CRM 최적화 프로젝트 - 쿠폰 발급 최적화

Trending Tags