Posts Data Structure Part1
Post
Cancel

Data Structure Part1

Posted Nov 29, 2020 2020-11-29T00:00:00+09:00 by Kwon Suncheol


통계학을 전공한 직후 데이터 분석 직군에서 일을 시작하면서 엄밀한 프로그래밍에 필요한 자료 구조와 알고리즘에 관하여 갈증 을 항상 느끼고 있었습니다. 이와 관련하여 반드시 알아야 할 자료 구조와 알고리즘을 차근히 사색하면서 정리하는 시간을 가지겠습니다. 이번 포스트에는 {Array, Queue, Stack, Linked List}에 대해 생각해보았습니다. 구체적인 구현 코드는 파이썬으로 작성하였습니다.

Queue

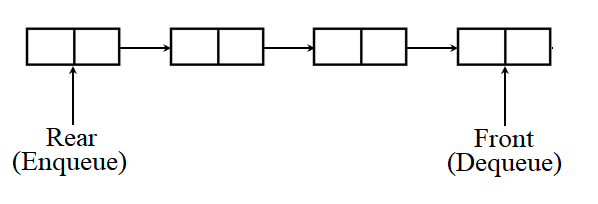
  • 큐(Queue)는 데이터가 들어온 순서대로 접근 가능합니다. 즉 FIFO(First in, First Out) 구조입니다.
  • 다음의 이미지를 통해 큐에 대하여 알 수 있습니다.

Queuehttps://www.baeldung.com/cs/types-of-queues1

큐(Queue)의 다음 기능을 구현하면 다음과 같습니다.

  • dequeue : 큐 앞쪽의 값을 반환한 뒤 제거합니다.
  • enqueue : 큐 뒤쪽에 값을 추가합니다.
  • front : 큐 앞쪽의 값을 조회합니다.
  • Isempty : 큐 값이 Null인지 확인합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Queue(object):    
    def __init__(self):
        self.objs = []
    def __len__(self):
        return len(self.objs)
    def __repr__(self):
        return repr(self.objs)    
    def enqueue(self,item):
        self.objs.insert(0,item)
    def dequeue(self):
        value = self.objs.pop()
        if value is not None:
            return value
        else:
            print('Queue가 비워 있습니다.')
    def front(self):
        if self.objs:
            return self.objs[-1]
        else:
            print('Queue가 비워 있습니다.')
    def isEmpty(self):
        return not bool(self.objs)

예시를 통해 Class Queue가 잘 구현되었는지 확인해보겠습니다.

1
2
3
4
5
6
7
8
9
10

if __name__ == "__main__":
    queue = Queue()
    print('큐가 비워있나요? : {}'.format(queue.isEmpty()))
    print('큐에 11부터 19까지 순서대로 추가합니다.')
    for i in range(11,20,1):
        queue.enqueue(i)
    print('큐의 크기는 다음과 같습니다 : {}'.format(len(queue)))
    print('한 값을 큐에서 뽑습니다 : {}'.format(queue.dequeue()))
    print('다음에 뽑힐 값을 확인합니다 : {}'.format(queue.front()))
    print('최종적인 큐의 값은 다음과 같습니다 : {}'.format(queue))

결과값은 다음과 같습니다.

1
2
3
4
5
6

큐가 비워있나요? : True
큐에 11부터 19까지 순서대로 추가합니다.
큐의 크기는 다음과 같습니다 : 9
한 값을 큐에서 뽑습니다 : 11
다음에 뽑힐 값을 확인합니다 : 12
최종적인 큐의 값은 다음과 같습니다 : [19, 18, 17, 16, 15, 14, 13, 12]

Stack

  • 스택(Stack)은 큐와 마찬가지로 데이터를 제한적으로 접근할 수 있습니다.
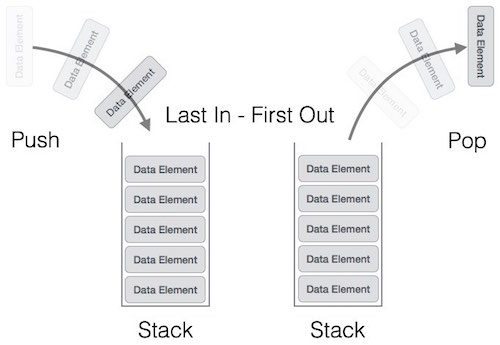
  • 하지만 큐와 다르게 LIFO(Last In, First Out) 구조입니다.
  • 스택의 이미지는 다음과 같습니다.

Stackhttps://www.tutorialspoint.com/data_structures_algorithms/stack_algorithm.htm2

스택의 다음 기능을 구현하면 다음과 같습니다.

  • push : 스택 맨 위에 값을 추가합니다.
  • pop : 스택 맨 아래 값을 반환하면서 제거합니다.
  • top : 스택 맨 아래 값을 조회합니다.
  • isempty : 스택의 값들이 비어 있는지 확인합니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22

class Stack:
    def __init__(self):
        self.objs = []
    def __len__(self):
        return len(self.objs)
    def __repr__(self):
        return repr(self.objs)
    def isempty(self):
        return not bool(self.objs)
    def push(self,item):
        self.objs.append(item)
    def pop_(self):
        val = self.objs.pop()
        if val is not None:
            return val
        else:
            print('스틱이 비워 있습니다.')
    def top(self):
        if self.objs:
            return self.objs[-1]
        else:
            print('스틱이 비워 있습니다.')

예시를 통해 Class Stack이 잘 구현되었는지 확인해보겠습니다.

1
2
3
4
5
6
7
8
9
10
11

if __name__ == "__main__":
    stack = Stack()
    print('스택이 비워있나요? : {}'.format(stack.isempty()))
    print('스택에 20부터 29까지 순서대로 추가합니다.')
    for i in range(20,30,1):
        stack.push(i)
    print('현재 스택의 값들은 다음과 같습니다 : {}'.format(stack))
    print('한 값을 스택에서 뽑습니다 : {}'.format(stack.pop_()))
    print('현재 남아 있는 스택의 값들은 다음과 같습니다 : {}'.format(stack))
    print('다음에 뽑힐 값을 확인합니다 : {}'.format(stack.top()))
    print('현재 남아 있는 스택의 크기는 다음과 같습니다 : {}'.format(len(stack)))

결과값은 다음과 같습니다.

1
2
3
4
5
6
7

스택이 비워있나요? : True
스택에 20부터 29까지 순서대로 추가합니다.
현재 스택의 값들은 다음과 같습니다 : [20, 21, 22, 23, 24, 25, 26, 27, 28, 29]
한 값을 스택에서 뽑습니다 : 29
현재 남아 있는 스택의 값들은 다음과 같습니다 : [20, 21, 22, 23, 24, 25, 26, 27, 28]
다음에 뽑힐 값을 확인합니다 : 28
현재 남아 있는 스택의 크기는 다음과 같습니다 : 9

위의 예시를 통해 우리는 스택 구조가 LIFO(Last-in,First-out) Queue와 같은 구조임을 확인할 수 있습니다.
흥미로운 점은 프로세스를 실행할 때 기본적으로 스택 구조로 진행된다는 점입니다.
간단한 재귀 함수(Recursive Function)를 만들어 프로세스의 스택 구조를 확인해 보겠습니다.

1

Array
  • 배열은 나열된 데이터를 인덱스에 대응하도록 구성한 데이터 구조입니다.
  • 그래서 데이터를 순차적으로 저장할 수 있고 빠른 접근이 가능하지만, 데이터가 가변적일 경우 데이터 구조 특성상 미리 최대 길이를 지정해야 하므로 데이터의 추가 및 삭제가 어렵습니다.
Linked List
  • 미리 길이를 지정해야 하는 Array와 다르게 연결 리스트(Linked List)는 산발적으로 분포되어 있는 데이터를 화살표로 연결하여 관리하는 데이터 구조입니다.
  • 본래 연결 리스트는 C언어에서 사용한 주요한 데이터 구조입니다. 하지만 파이썬은 리스트 타입이 연결 리스트의 기능을 모두 지원합니다.
  • 연결 리스트는 크게 노드(Node)들로 구성되어 있습니다.
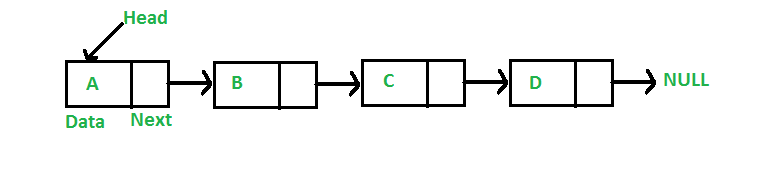
  • 노드는 다시 데이터 저장 단위로 구체적인 데이터값과 각 노드 안에서, 다음의 노드와의 연결 정보를 함축하고 있는 공간인 포인터(Pointer)로 이루어져 있습니다.
    • 구조상 당연히 리스트의 마지막 포인터는 Null값입니다.
연결 리스트의 이미지를 살펴보면 다음과 같습니다.
Linked_Listhttps://www.geeksforgeeks.org/data-structures/linked-list/3
먼저 포인터를 활용해 Node와 Node를 연결해 보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12

class Node:
    # 인자를 데이터 하나만 쓰면 next값은 'None'입니다.
    # 만약 인자에 data와 next를 넣어 주면 데이터와 주소값이 들어갑니다.
    def __init__(self, data, next=None):
        self.data = data
        self.next = next
def add(data):
    # 가장 앞에 있는 노드를 head 객체에 담습니다.
    node = head
    while node.next:
        node = node.next
    node.next = Node(data)   

링크드 리스트로 데이터를 추가한 함수(add())가 정상 작동하는지 확인해보겠습니다.
1
2
3
4
5
6
7
8
9

node1 = Node(1)

for idx in range(2,15):
	add(idx) # 2부터 14까지의 데이터를 추가합니다.
node = head
while node.next:
	print(node.data)
	node = node.next
print(node.data)

해당 예시에서 결과는 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14

1
2
3
4
5
6
7
8
9
10
11
12
13
14

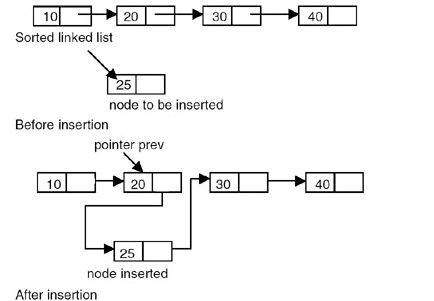
자연스럽게 다음의 상황을 생각할 수 있습니다.
insert_into_sorted_listhttps://engineering.purdue.edu/~milind/ece264/2017spring/assignments/pa09/4
만약 위와 같이 링크드 리스트 구조인 [10,20,30,40] 에서 20과 30 사이에 25를 넣기 위해서 어떻게 해야할까요? 이를 해결하기 위한 코드를 만들기 전에 링크드 리스트 데이터에 어떤 값을 추가할 경우 더할 수 있는 경우의 수를 고려해 보면 다음과 같습니다.
  • 첫번째 노드 전에 추가하는 경우.
  • 중간 노드들 사이에 추가하는 경우.
  • 마지막 노드 다음에 추가하는 경우.
위의 이미지는 두번째 케이스(중간 노드들 사이에 추가하는 경우)에 속합니다. 이를 우선 간단히 코드화 해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28

node1 = Node(10)
head = node1
for index in range(20,50,10):
    add(index)    
  
node = head
while node.next:
    print(node.data)
    node = node.next
node3 = Node(25)

node = head
node_search = True
while node_search:
    if node.data == 20:
        node_search = False
    else:
        node = node.next

node_next = node.next
node.next = node3
node3.next = node_next

node = head
while node.next:
    print(node.data)
    node = node.next
print(node.data)

다행히 원하는 결과값이 나옵니다.
1
2
3
4
5

10
20
25
30
40

다음으로 위의 세 가지 경우를 모두 충족할 수 있도록 코드화해보면 다음과 같습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24

class Node:
    def __init__(self, data, next=None):
        self.data = data
        self.next = next
    
class NodeConnect:
    def __init__(self, data):
        self.head = Node(data)
    
    def add(self, data):
        if self.head == '':
            self.head = Node(data)
        else:
            node = self.head
            while node.next:
                node = node.next
            node.next = Node(data)

    # 해당 링크드 리스트 데이터를 출력하는 함수
    def print_node(self):
        node = self.head
        while node:
            print(node.data)
            node = node.next

처음의 노드값을 0으로 준 뒤 1부터 9까지의 값을 링크드 리스트로 연결해 보면 다음과 같이 출력됨을 확인할 수 있습니다.
1
2
3
4

linkedlist1 = NodeConnect(0)
for data in range(1, 10):
    linkedlist1.add(data)
linkedlist1.print_node()

1
2
3
4
5
6
7
8
9
10

0
1
2
3
4
5
6
7
8
9

그렇다면 특정 노드를 삭제하기 위해서는 어떻게 해야 할까요?
 삭제도 다음의 세 가지 경우가 있습니다.
  • 첫번째 노드를 삭제할 경우.
  • 중간 노드를 삭제할 경우.
  • 마지막 노드를 삭제할 경우.
이를 고려하여 구현해보겠습니다.
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45

class Node:
    def __init__(self, data, next=None):
        self.data = data
        self.next = next
    
class NodeConnect:
    def __init__(self, data):
        self.head = Node(data)
        
    def add(self, data):
        if self.head == '':
            self.head = Node(data)
        else:
            node = self.head
            while node.next:
                node = node.next
            node.next = Node(data)
        
    def print_node(self):
        node = self.head
        while node:
            print (node.data)
            node = node.next
    
    def delete(self, data):
        if self.head == '':
            print("해당 값을 가진 노드가 없습니다.")
            return False
        
        # 첫번째 노드를 삭제할 경우
        if self.head.data == data:
            temp = self.head
            self.head = self.head.next
            del temp
        # 중간 노드와 마지막 노드를 삭제할 경우
        else:
            node = self.head
            while node.next:
                if node.next.data == data:
                    temp = node.next
                    node.next = node.next.next
                    del temp
                    return
                else:
                    node = node.next


지금까지 다양한 자료 구조들 중에서 {Array, Queue, Stack, Linked List}를 코드를 통해 생각해 보았습니다. 처음에는 쉬운 참고 자료5를 통해 직관적으로 자료구조들을 공부할 수 있었습니다. 하지만 위의 자료 구조들을 직접 구현해 보면서 다음의 명제를[“각각의 데이터 자료 구조별로 장단점이 존재하기 때문에 프로그래밍을 할 때 맥락에 맞는 자료 구조를 선택하는 것이 중요하다” ]를 보다 분명하게 발견할 수 있었습니다. 무엇보다 프로그래밍 관련된 부분을 공부하고 사고할수록 과거의 옳지 못했던 코딩 습관을 되돌아볼 수 있어서 굉장히 재밌습니다. ‘자료 구조’와 ‘알고리즘’ 관련하여 계속해서 공부하고 연결하고 싶은 마음을 간직하면서 짧은 글을 마무리 하겠습니다.

Reference
  1. https://www.baeldung.com/cs/types-of-queues ↩
  2. https://www.tutorialspoint.com/data_structures_algorithms/stack_algorithm.htm ↩
  3. https://www.geeksforgeeks.org/data-structures/linked-list/ ↩
  4. https://engineering.purdue.edu/~milind/ece264/2017spring/assignments/pa09/ ↩
  5. https://visualgo.net/en/list ↩
  Data_Structure
  data structure stack queue linked_list
 This post is licensed under CC BY 4.0 by the author.
Contents
 
-
 
Kernel Density Estimation